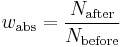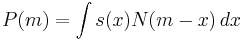Fitness (biology)

Fitness (often denoted 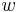w in population genetics models) is a central idea in evolutionary theory. It can be defined either with respect to a genotype or to a phenotype. In either case, it is equal to the average contribution to the gene pool of the next generation that is made by an average individual of the specified genotype or phenotype. If differences between alleles at a given gene affect fitness, then the frequencies of the alleles will change over generations; the alleles with higher fitness become more common. This process is called natural selection.

An individual's fitness is manifested through its phenotype. As phenotype is affected by both genes and environment, the fitnesses of different individuals with the same genotype are not necessarily equal, but depend on the environment in which the individuals live. However, since the fitness of the genotype is an averaged quantity, it will reflect the reproductive outcomes of all individuals with that genotype.

Inclusive fitness differs from individual fitness by including the ability of an allele in one individual to promote the survival and/or reproduction of other individuals that share that allele, in preference to individuals with a different allele. One mechanism of inclusive fitness is kin selection.

Contents

Measures of fitness

There are two commonly used measures of fitness; absolute fitness and relative fitness.

Absolute fitness

Absolute fitness (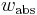w_{\mathrm{abs}}) of a genotype is defined as the ratio between the number of individuals with that genotype after selection to those before selection. It is calculated for a single generation and may be calculated from absolute numbers or from frequencies. When the fitness is larger than 1.0, the genotype increases in frequency; a ratio smaller than 1.0 indicates a decrease in frequency.

{w_{\mathrm{abs}}} = {{N_{\mathrm{after}}} \over {N_{\mathrm{before}}}}

Absolute fitness for a genotype can also be calculated as the product of the proportion survival times the average fecundity.

Relative fitness

Relative fitness is quantified as the average number of surviving progeny of a particular genotype compared with average number of surviving progeny of competing genotypes after a single generation, i.e. one genotype is normalized at 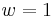w=1 and the fitnesses of other genotypes are measured with respect to that genotype. Relative fitness can therefore take any nonnegative value, including 0.

While researchers can usually measure relative fitness, absolute fitness is more difficult. It is often difficult to determine how many individuals of a genotype there were immediately after reproduction.

The two concepts are related, and both of them are equivalent when they are divided by the mean fitness, which is weighted by genotype frequencies.

{\frac{w_{abs}}{\overline{w}_{abs}} = \frac{w_{rel}}{\overline{w}_{rel}}}

Because fitness is a coefficient, and a variable may be multiplied by it several times, biologists may work with "log fitness" (particularly so before the advent of computers). By taking the logarithm of fitness each term may be added rather than multiplied.

Maynard-Smith's Definition

As another example we may mention the definition of fitness given by Maynard Smith in the following way: "Fitness is a property, not of an individual, but of a class of individuals – for example homozygous for allele A at a particular locus. Thus the phrase ’expected number of offspring’ means the average number, not the number produced by some one individual. If the first human infant with a gene for levitation were struck by lightning in its pram, this would not prove the new genotype to have low fitness, but only that the particular child was unlucky." [1]

Hartl's Definition

Yet another possible measure has been formulated: "The fitness of the individual - having an array x of phenotypes - is the probability, s(x), that the individual will be included among the group selected as parents of the next generation." Then, the mean fitness may be determined as a mean over the set of individuals in a large population.

P(m) = \int s(x) N(m - x)\, dx [2]

where N is the probability distribution function of phenotypes in the population, and m is its centre of gravity. This measure is a suitable basis of a model of an evolution selecting individuals. It may in principle take even the stroke of the lightning into consideration. In the case N is a Gaussian it is fairly easily proved that the average information (information entropy, disorder, diversity) of a large population may be maximized by Gaussian adaptation - keeping the mean fitness constant - in accordance with recapitulation, the central limit theorem, the Hardy-Weinberg law and the second law of thermodynamics. This is in contrast to Fisher's fundamental theorem of natural selection.

History

The British sociologist Herbert Spencer coined the phrase "survival of the fittest" (though originally, and perhaps more accurately, "survival of the best fitted") in his 1851 work Social Statics and later used it to characterise what Charles Darwin had called natural selection.

The British biologist J.B.S. Haldane was the first to quantify fitness, in terms of the modern evolutionary synthesis of Darwinism and Mendelian genetics starting with his 1924 paper A Mathematical Theory of Natural and Artificial Selection. The next further advance was the introduction of the concept of inclusive fitness by the British biologist W.D. Hamilton in 1964 in his paper on The Evolution of Social Behavior.

Fitness landscape

A fitness landscape, first conceptualized by Sewall Wright, is a way of visualising fitness in terms of a high-dimensional surface, in which height indicates fitness, and each of the other dimensions represents allele identity for a different gene. Peaks correspond to local fitness maxima; it is often said that natural selection always progresses uphill but can only do so locally. This can result in suboptimal local maxima becoming stable, because natural selection cannot return to the less-fit "valleys" of the landscape on the way to reach higher peaks.

Genetic load

Genetic load measures the average fitness of a population of individuals, relative to a hypothetical population in which the most fit genotype has become fixed.

See also

Notes

  1. ↑ Maynard-Smith, J. (1989) Evolutionary Genetics ISBN 0198542151
  2. ↑ Hartl, D. L. (1981) A Primer of Population Genetics ISBN 0878932712

Further reading

External links